5,00 von 5 Sterne
Loading...
Fibonacci-Zahlen begegnen uns überall – in der Mathematik, in Pflanzen und sogar im Alltag.
In diesem Artikel lernst du die Fibonacci-Folge Schritt für Schritt kennen, bekommst einfache Beispiele und eine Formel zum Selberrechnen.
So verstehst du schnell, warum Fibonacci-Zahlen ein besonderes Natur- und Mathephänomen sind. Wenn dir Mathe oft kompliziert erscheint, hilft dir dieser Artikel, das Thema verständlich und ohne Fachsprache zu durchschauen.
Fibonacci-Zahlen sind eine besondere Zahlenfolge, bei der immer zwei Nachbarzahlen addiert werden, um die nächste Zahl zu erhalten. Sie startet mit 0 und 1 – und danach geht’s los.
Kurz erklärt:
0, 1, 1, 2, 3, 5, 8, 13, 21, …
Jede Zahl entsteht aus der Summe der beiden vorherigen. Klingt simpel, hat aber enorme Bedeutung in Mathe, Natur und Technik.
Exkurs: Wer war Fibonacci und wie entstand die Folge?
Fibonacci, eigentlich Leonardo von Pisa, lebte am 12. und 13. Jahrhundert in Italien. Er war einer der bedeutendsten Mathematiker seiner Zeit und brachte viele arabische Zahlensysteme nach Europa.
Die Fibonacci-Folge entstand in seinem Buch Liber Abaci von 1202. Darin stellte er eine Aufgabe: Wie viele Kaninchenpaare entstehen in einem Jahr, wenn jedes Paar nach einem Monat ein neues Paar zeugt?
Die Lösung führte zu einer Zahlenreihe, die heute als Fibonacci-Folge bekannt ist: 0, 1, 1, 2, 3, 5, 8 …
Fibonacci entdeckte also die Folge nicht nur als abstraktes Mathe-Phänomen, sondern als praktische Lösung für ein Wachstumsproblem, das die Natur in vielen Formen widerspiegelt.
Fibonacci-Folge – Einfach erklärt
Die Fibonacci-Folge ist eine rekursive Zahlenfolge. Das bedeutet: Jede neue Zahl hängt von den vorherigen ab.
Warum ist das wichtig?
Viele reale Vorgänge – Wachstum, Muster, Verzweigungen – funktionieren nach dem gleichen Prinzip.
Fibonacci-Zahlen Tabelle – Zahlenreihen auf einen Blick
Damit du sofort siehst, wie sich die Folge entwickelt, hier eine Übersicht der ersten 15 Fibonacci-Zahlen:
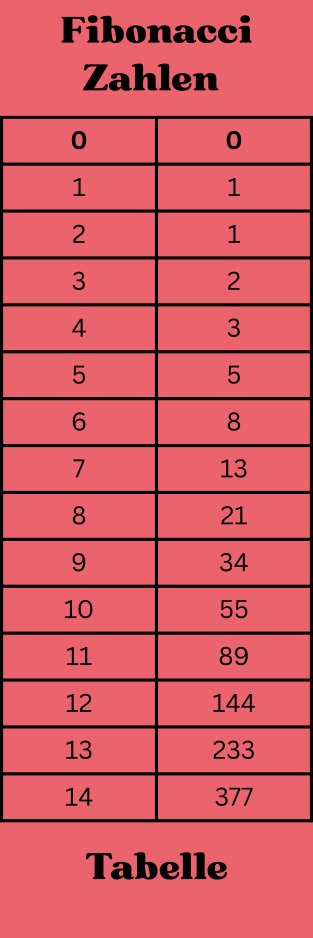
Merke: Die Zahlen wachsen schneller, als man denkt.
Fibonacci-Folge Formel – Fibonacci-Zahlen berechnen
Es gibt verschiedene Wege, Fibonacci-Zahlen zu berechnen. Hier ist die einfachste Formel:
Fn = F(n–1) + F(n–2)
Um die nächste Fibonacci-Zahl zu bekommen, addierst du die zwei vorherigen Zahlen.
- F(n) = die n-te Fibonacci-Zahl
- n = die Position in der Reihenfolge
- F(n–1) = die Fibonacci-Zahl eine Position davor
- F(n–2) = die Fibonacci-Zahl zwei Positionen davor
Beispiel:
Willst du die 7. Fibonacci-Zahl ausrechnen?
- F5 = 5
- F6 = 8
- F7 = 13
→ 5 + 8 = 13
Die schnelle Formel (Binet-Formel) – für Fortgeschrittene
Wenn du schon etwas weiter bist, gibt es sogar eine direkte Formel:
Fn = (φⁿ – (–φ)⁻ⁿ) / √5,
wobei φ ≈ 1,618 die Goldene Zahl ist.
Für den Unterricht reicht aber die einfache Additions-Regel völlig aus.
Fibonacci-Zahlen im Alltag – wo du sie wirklich brauchst
Fibonacci klingt oft theoretisch – ist es aber nicht. Viele Anwendungen begegnen uns ständig:
Smartphone-Kameras & Bildbearbeitung
Fotobearbeitungs-Apps nutzen „goldene“ Proportionen, um Bilder ansprechend zu gestalten. Fibonacci spielt hier eine große Rolle.
Suchalgorithmen & Computerprogramme
Bei Sortieralgorithmen oder Datenstrukturen tauchen Fibonacci-Zahlen als effiziente Rechenwege auf.
Musik & Rhythmus
Viele Komponisten nutzen Fibonacci-Längen, um Musik natürlicher wirken zu lassen.
Mini-Beispiel:
Ein Stück wird in 2-, 3- oder 5-Takt-Gruppen aufgebaut — das ergibt harmonische Muster.
Fibonacci-Zahlen in der Natur – das berühmte Naturphänomen
In der Natur treten Fibonacci-Zahlen überraschend häufig auf. Pflanzen und Tiere entwickeln Strukturen, die nach Fibonacci aufgebaut sind — weil sie Wachstum effizient machen.
Typische Beispiele aus der Natur:
- Blütenblätter: Viele Pflanzen haben 3, 5, 8, 13 oder 21 Blätter.
- Tannenzapfen: Die Spiralen laufen oft in Fibonacci-Richtungen.
- Sonnenblumen: Ihre Kerne wachsen in zwei Fibonacci-Spiralen – das spart Platz.
- Schneckenhäuser: Die wachsende Spirale folgt dem „Goldenen Winkel“.
- Pflanzenwachstum: Neue Blätter entstehen in Winkeln, die Fibonacci-Muster bilden.
Warum macht die Natur das?
Fibonacci ermöglicht maximale Nutzung von Raum und Licht – eine perfekte Strategie fürs Überleben.
Fazit
Die Fibonacci-Zahlen sind viel mehr als eine mathematische Folge. Sie helfen dir, Wachstum, Muster und Strukturen in unserer Welt besser zu verstehen. Ob Natur, Technik oder Kunst – überall steckt ein Stück Fibonacci drin.
