Abc-Formel einfach erklärt: in 5 Minuten verstehen

(Noch keine Bewertungen)

Du musst eine quadratische Gleichung lösen und weisst nicht genau, wie die abc-Formel funktioniert? In diesem Artikel erklären wir dir einfach, wie du die Formel anwendest, mit Beispielen zum Nachrechnen und typischen Fehlern, die du vermeiden solltest.

Inhalt

Erklärung und Grundlagen

Mit der abc-Formel kann man quadratische Gleichungen mit der Form f(x) = ax² + bx + c lösen.

Man braucht sie, um Nullstellen der quadratischen Funktion zu bestimmen.

Wie lautet die abc-Formel?

$x1,2=\frac{-b\pm\sqrt{b2-4ac}}{2a}$

Damit kann man die Ergebnisse x1 und x2 berechnen. Dafür setzt man die Werte für a, b und c ein und rechnet das Ergebnis einmal mit + und einmal mit – aus.

Der Teil unter der Wurzel, also $\sqrt{b^2 - 4ac}$ ist die Diskriminante (D). Sie entscheidet, wie viele und welche Art von Lösungen es gibt.

D > 0 zwei verschiedene Lösungen
D = 0 eine Lösung
D < 0 keine reelle Lösung

Abgrenzung zu anderen Formeln – wo liegt der Unterschied?

Neben der abc-Formel hast du bestimmt schonmal von der pq-Formel gehört.
Sie gilt für Gleichungen der Form x² + px + q = 0

Die pq Formel lautet:

$x_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 - q}$

Die pq-Formel ist etwas einfacher als die abc-Formel, sie funktioniert aber nur wenn der Faktor vor x² gleich 1 ist. Die abc-Formel funktioniert egal welche Zahl vor dem x² steht.

Bedingungen für die Anwendung der abc Formel

Damit du die abc-Formel richtig anwenden kannst, muss es sich um eine quadratische Gleichung in der Form ax² + bx + c = 0 mit a ≠ 0 handeln

Die praktische Anwendung der abc Formel

Damit du die abc-Formel besser verstehst, schauen wir uns ein Beispiel an:

x² + 6 = – 5x

Wir zeigen dir Schritt für Schritt, wie du die Formel anwendest.

1. Gleichung gleich 0 setzen

$x^2 + 6 = -5x \quad | +5x\\ x^2 + 5x + 6 = 0\\$

2. Koeffizienten a, b und c ablesen

$a = 1, \quad b = 5, \quad c = 6\\$

3. Koeffizienten in die abc-Formel einsetzen

$x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\ x_{1,2} = \frac{-5 \pm \sqrt{5^2 - 4 \cdot 1 \cdot 6}}{2 \cdot 1}\\$

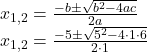
4. Ergebnisse ausrechnen

$x_{1,2} = \frac{-5 \pm \sqrt{25 - 24}}{2}\\ x_{1,2} = \frac{-5 \pm \sqrt{1}}{2}\\ x_{1,2} = \frac{-5 \pm 1}{2}x_1 = \frac{-5 + 1}{2} = \frac{-4}{2} = -2\\ \quad\quad x_2 = \frac{-5 - 1}{2} = \frac{-6}{2} = -3\\$

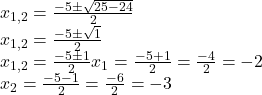
5. Nullstellen

$x_1 = -2, \quad x_2 = -3$

Typische Fehlerquellen der abc-Formel

Beim Rechnen passieren oft kleine Fehler. Das ist normal und passiert jedem mal, ist aber vermeidbar. Deswegen solltest du besonders darauf achten:

Vorsicht bei Vorzeichen beim Einsetzen in die Formel
Vorsicht beim Wurzelziehen!
Den Zähler beim Teilen in Klammern setzen → Den ganzen Zähler durch 2a teilen!

Übungsaufgaben zur abc-Formel

Hast du alles verstanden? Teste dein Wissen mit diesen Übungsaufgaben!

Aufgabe 1: Bestimme die Nullstellen der quadratischen Funktion

$\; 2x^2 + 6 = 8x$

$1. \; \textbf{Gleichung\ gleich\ 0\ setzen:}\\ 2x^2 + 6 = 8x \quad | -8x\\ 2x^2 + 6 - 8x = 0//2x^2 - 8x + 6 = 0\\ \\ 2. \; \textbf{Koeffizienten\ a\, b\ und\ c\ ablesen:}\\a = 2, \quad b = -8, \quad c = 6\\ \\ 3. \; \textbf{Koeffizienten\ in\ die\ Mitternachtsformel\ einsetzen:}\\ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\ x_{1,2} = \frac{8 \pm \sqrt{(-8)^2 - 4 \cdot 2 \cdot 6}}{2 \cdot 2} \]\\ \\ 4. \; \textbf{Ergebnisse\ ausrechnen:}\\x_{1,2} = \frac{8 \pm \sqrt{64 - 48}}{4}\\ x_{1,2} = \frac{8 \pm \sqrt{16}}{4}\\ x_{1,2} = \frac{8 \pm 4}{4} \\x_1 = \frac{8+4}{4} = 3\quad\quad\x_2 = \frac{8-4}{4} = 1\\ \\ 5. \; \textbf{Nullstellen:} x_1 = 3, \quad x_2 = 1 \]$

Aufgabe 2: Bestimme die Nullstellen der quadratischen Funktion

$\;2x^2 - 5x = -3\\ 1. \; \textbf{Gleichung\ gleich\ 0\ setzen:}\\2x^2 - 5x = -3 \quad | +3\\ 2x^2 - 5x + 3 = 0\\ \\ 2. \; \textbf{Koeffizienten\ a\, b\ und\ c\ ablesen:}\\ a = 2, \quad b = -5, \quad c = 3\\ \\ 3. \; \textbf{Koeffizienten\ in\ die\ Mitternachtsformel\ einsetzen:} \\ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\ x_{1,2} = \frac{5 \pm \sqrt{(-5)^2 - 4 \cdot 2 \cdot 3}}{2 \cdot 2}\\ \\ 4. \; \textbf{Ergebnisse\ ausrechnen:}\\ x_{1,2} = \frac{5 \pm \sqrt{25 - 24}}{4}\\ x_{1,2} = \frac{5 \pm \sqrt{1}}{4}\\ x_{1,2} = \frac{5 \pm 1}{4}\\ x_1 = \frac{5+1}{4} = \frac{6}{4} = 1{,}5 \quad\quadx_2 = \frac{5-1}{4} = \frac{4}{4} = 1\\ \\ 5. \; \textbf{Nullstellen:}\\ x_1 = 1{,}5, \quad x_2 = 1$

FAQ

Was ist die Mitternachtsformel?

Die Mitternachtsformel ist einfach nur ein anderer Begriff für die abc-Formel.

Wie lautet die pq-Formel?

$x_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 - q}$

Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung hinterlässt. Vielen Dank!
(Noch keine Bewertungen)
Loading...

Abc-Formel einfach erklärt: in 5 Minuten verstehen