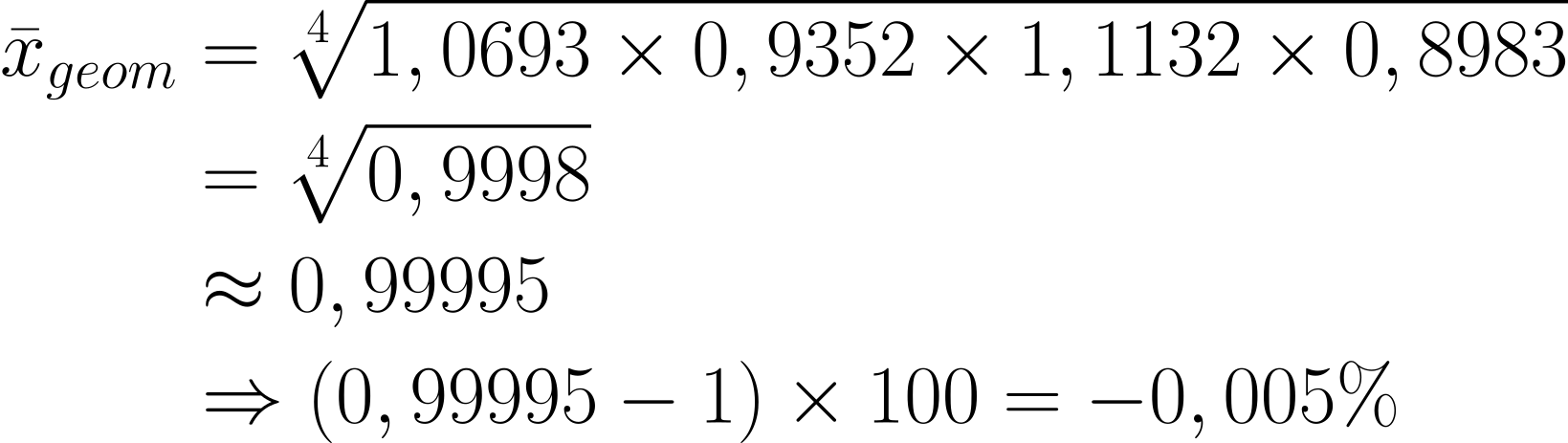Hast du schon mal vom geometrischen Mittel gehört, weißt aber noch nicht so genau, was das eigentlich ist? Keine Sorge!
In diesem Artikel lernst du einfach und verständlich:
- Was das geometrische Mittel genau ist (Definition).
- Wie du die Formel korrekt anwendest, um das geometrische Mittel zu berechnen.
- Worin die entscheidenden Unterschiede zum arithmetischen und harmonischen Mittel liegen.
- Wie du dein Wissen mit einigen Übungsaufgaben festigen kannst.
Legen wir gleich los!
Was ist das geometrische Mittel?
Das geometrische Mittel ist ein sogenannter Lageparameter aus der deskriptiven Statistik. Vereinfacht gesagt, ist es ein spezieller Durchschnitt, der immer dann verwendet wird, wenn du die mittlere prozentuale Veränderung von Werten berechnen willst.
Die Anwendung ist daher ideal für die Analyse von Wachstumsraten, wie zum Beispiel bei der Preissteigerung über mehrere Jahre oder Monate oder bei der Berechnung der durchschnittlichen Rendite von Geldanlagen mit Zinsraten.

Was bedeuten die Symbole in der Formel des Geometrischen Mittels?
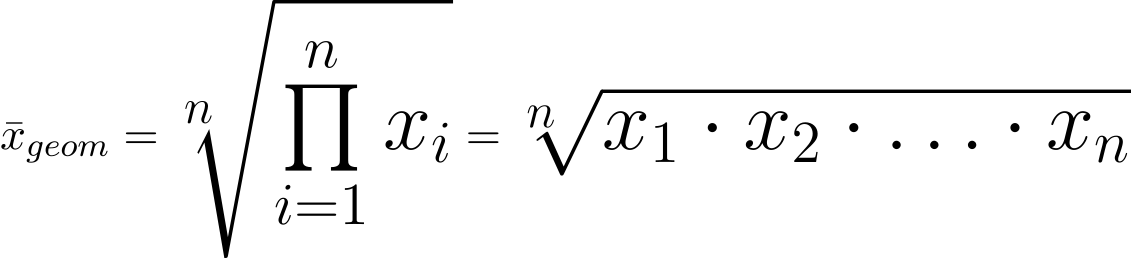
Keine Panik! Das sieht komplizierter aus, als es ist.
Im Grunde tust du nur zwei Dinge:
- Multiplizieren: Du multiplizierst alle deine Werte (
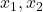 usw.) miteinander und erhältst ein Produkt.
usw.) miteinander und erhältst ein Produkt. - Wurzel ziehen: Aus diesem Produkt ziehst du die n-te Wurzel, wobei
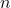 die Anzahl deiner Werte ist.
die Anzahl deiner Werte ist.
In der Mathematik wird das Multiplizieren vieler Zahlen oft mit dem Produktzeichen ![]() (dem griechischen Buchstaben Pi) abgekürzt. Es ist der “Bruder” des bekannten Summenzeichens
(dem griechischen Buchstaben Pi) abgekürzt. Es ist der “Bruder” des bekannten Summenzeichens ![]() . Die Formel sieht dann so aus:
. Die Formel sieht dann so aus:
![]()
![]() : Das ist das Symbol für das geometrische Mittel. Es setzt sich so zusammen:
: Das ist das Symbol für das geometrische Mittel. Es setzt sich so zusammen:
- Der Balken über dem x (
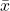 ) ist das allgemeine mathematische Zeichen für einen Mittelwert (Durchschnitt).
) ist das allgemeine mathematische Zeichen für einen Mittelwert (Durchschnitt). - Der tiefgestellte Zusatz geom steht für „geometrisch“ und stellt klar, dass es sich nicht um das arithmetische oder harmonische Mittel handelt.
Die kleinen Symbole am Produktzeichen erklären dabei den genauen “Weg” der Multiplikation:
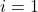 (unten): Das ist der Startpunkt. Du beginnst die Multiplikation beim ersten Wert (
(unten): Das ist der Startpunkt. Du beginnst die Multiplikation beim ersten Wert (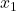 ).
).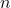 (oben): Das ist der Endpunkt. Du multiplizierst so lange, bis du beim letzten Wert (
(oben): Das ist der Endpunkt. Du multiplizierst so lange, bis du beim letzten Wert (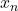 ) angekommen bist.
) angekommen bist.
Wenn wir also beispielsweise drei Werte haben, dann ist n = 3. Die allgemeine Formel schlüsselt sich dann wie folgt auf:
![]()
- Bei einer Zunahme rechnest du:
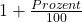
- Bei einer Abnahme rechnest du:
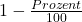
Beispiele:
- Eine Zunahme um 10 % wird zum Wachstumsfaktor 1,1.
- Eine Abnahme um 10 % wird zum Wachstumsfaktor 0,9.
- Eine Zunahme um 5 % wird zum Wachstumsfaktor 1,05.
Geometrisches Mittel berechnen:
Anwendungsbeispiel Wachstumsfaktor

Mit einem Beispiel ist es einfach erklärt. Stell dir vor, die Preise für einen Döner haben sich in den letzten Monaten wie folgt entwickelt:
| Mai | Juni | Juli | August | September |
| 3,20 € | 3,80 € | 4,10 € | 3,70 € | 4,20 € |
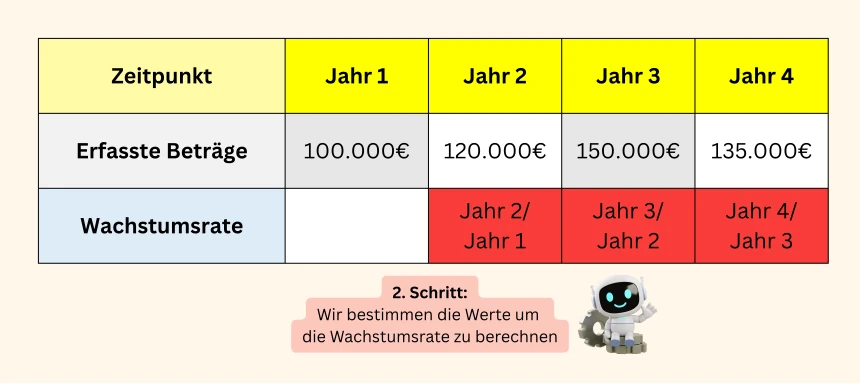
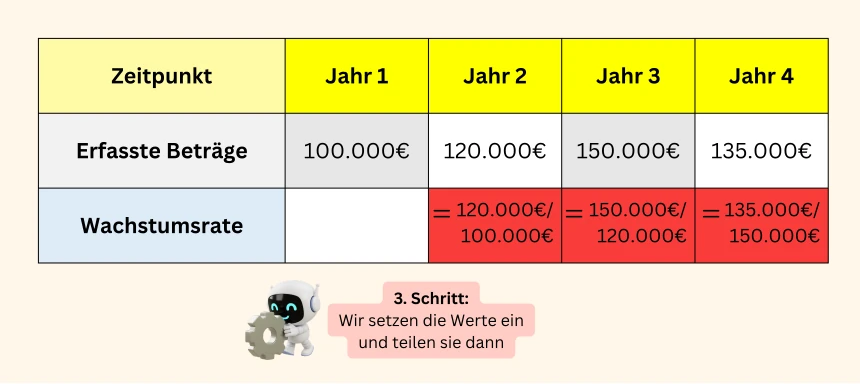
Berechnung der Wachstumsfaktoren
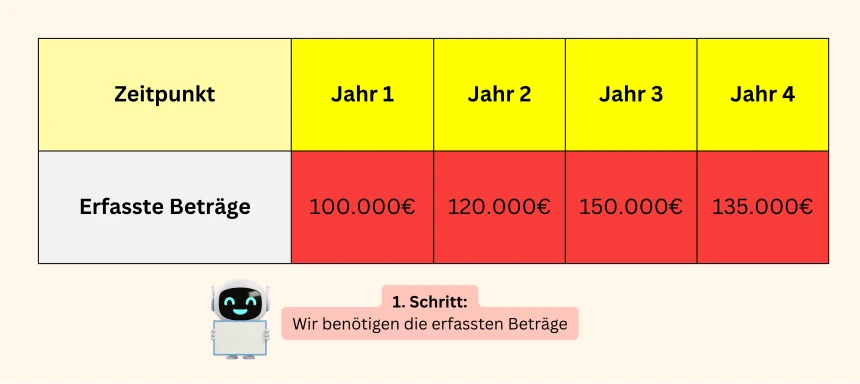
Schritt 1: Um das geometrische Mittel zu berechnen, brauchen wir die Wachstumsfaktoren für jeden Monat. Es gibt zwei gängige Wege, um diese zu ermitteln:
Möglichkeit 1: Der direkte Weg
Du kannst den Wachstumsfaktor direkt berechnen, indem du den neuen Preis durch den Preis des Vormonats teilst.
Die Formel dafür lautet: ![]()
- Juni:
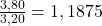
- Juli:
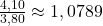
- … und so weiter.
Möglichkeit 2: Über die prozentuale Veränderung
Alternativ berechnest du zuerst die prozentuale Veränderung und wandelst diese dann in einen Wachstumsfaktor um.
Dafür berechnest du die monatliche Veränderung, indem du den Preis des Vormonats vom aktuellen Preis abziehst und das Ergebnis durch den Preis des Vormonats teilst.
Die Formel dafür lautet: ![]()
- Juni:
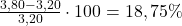
- Juli:
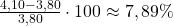
- August:
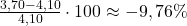
- September:
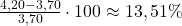
| Juni | Juli | August | September |
| 18,75 % | 7,89 % | -9,76 % | 13,51 % |
Diese Prozentzahlen wandelst du anschließend wie bekannt in Wachstumsfaktoren um (z.B. 1 + 18,75 / 100 = 1,1875).
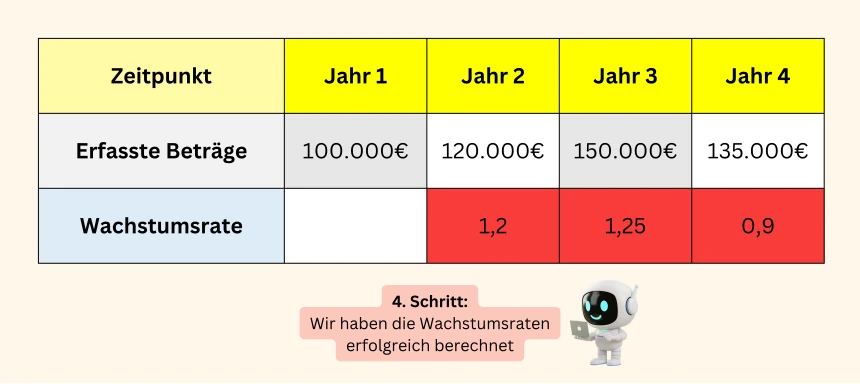
Egal welchen Weg du wählst, du erhältst die gleichen vier Wachstumsfaktoren, mit denen wir jetzt weiterrechnen: 1,1875, 1,0789, 0,9024 und 1,1351.
Nun ist die Frage: Wie hat sich der Preis für Döner im Durchschnitt prozentual verändert?
Werte einsetzen und das geometrische Mittel berechnen
Schritt 2: Jetzt, wo wir unsere Wachstumsfaktoren haben, setzen wir sie Schritt für Schritt in die Formel ein.
- Die allgemeine Formel: Der Ausgangspunkt ist immer die allgemeine Formel mit dem Produktzeichen.
![Rendered by QuickLaTeX.com \bar{x}_{geom} = \sqrt[n]{\prod_{i=1}^{n} x_i}](https://www.nachhilfe-team.net/lernen-leicht-gemacht/wp-content/ql-cache/quicklatex.com-ca0724acdee37f4a5fd79145835994ef_l3.png)
- Die Formel für unseren Fall aufschlüsseln: Wir haben 4 Werte, also ist
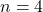 . Wir setzen die Werte in die Formeln ein:
. Wir setzen die Werte in die Formeln ein: ![Rendered by QuickLaTeX.com \bar{x}_{geom} = \sqrt[4]{\prod_{i=1}^{4} x_i} = \sqrt[4]{1,1875 \cdot 1,0789 \cdot 0,9024 \cdot 1,1351}](https://www.nachhilfe-team.net/lernen-leicht-gemacht/wp-content/ql-cache/quicklatex.com-6240434ddc75da8daa06657a50fe0d9f_l3.png)
- Zahlen unter der Wurzel multiplizieren: Nun berechnen wir das Produkt der Zahlen unter der Wurzel:
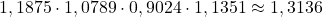 Unsere Formel vereinfacht sich zu:
Unsere Formel vereinfacht sich zu: ![Rendered by QuickLaTeX.com \bar{x}_{geom} = \sqrt[4]{1,3136}](https://www.nachhilfe-team.net/lernen-leicht-gemacht/wp-content/ql-cache/quicklatex.com-9e8d287463db0437c9dc1b92c3e521fb_l3.png)
- Die Wurzel ziehen: Zuletzt ziehen wir die 4. Wurzel aus dem Ergebnis. Dies ist der durchschnittliche Wachstumsfaktor:
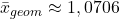
Das bedeutet, dass der Preis für Döner sich im Durchschnitt um 7% verändert hat.

Geometrisches, Arithmetisches & Harmonisches Mittel: Der Unterschied
Alle drei sind “Mittelwerte“, aber sie werden für völlig unterschiedliche Situationen gebraucht. Den falschen Mittelwert zu wählen, führt schnell zu einem falschen Ergebnis. Der Unterschied ist aber einfach zu merken.
Das Arithmetische Mittel – Der “normale” Durchschnitt
Das ist der Durchschnitt, den du von Schulnoten kennst. Du addierst einfach alle Werte und teilst die Summe durch die Anzahl der Werte (mehr Infos).
- Wann verwenden? Für unabhängige Werte, die sich nicht gegenseitig beeinflussen, wie z.B. Körpergrößen oder die tägliche Niederschlagsmenge.
- Beispiel: Du schreibst in drei Tests die Noten 2, 3 und 4. Dein Notendurchschnitt ist
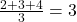 .
. - Formel:
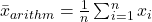
Das Geometrische Mittel – Der Durchschnitt für Wachstumsraten
Wie wir im Artikel gelernt haben, ist das die richtige Wahl für Werte, die aufeinander aufbauen, also multiplikativ zusammenhängen.
- Wann verwenden? Für die Berechnung von durchschnittlichen Wachstumsraten, Zinsen oder prozentualen Veränderungen über die Zeit.
- Beispiel: Das Wachstum deines Investments betrug im ersten Jahr +10 % (Faktor 1,1) und im zweiten +20 %(Faktor 1,2). Das durchschnittliche Wachstum ist das geometrische Mittel.
- Formel:
![Rendered by QuickLaTeX.com \bar{x}_{geom} = \sqrt[n]{\prod_{i=1}^{n} x_i}](https://www.nachhilfe-team.net/lernen-leicht-gemacht/wp-content/ql-cache/quicklatex.com-ca0724acdee37f4a5fd79145835994ef_l3.png)
Das Harmonische Mittel – Der Durchschnitt für Verhältnisse
Das harmonische Mittel brauchst du immer dann, wenn es um Verhältnisse oder Raten geht.
- Wann verwenden? Typischerweise bei Geschwindigkeiten (km/h), Preisen pro Einheit (€/Liter) oder Durchflussraten (Liter/Minute).
- Beispiel: Du fährst eine Strecke mit 50 km/h hin und mit 100 km/h zurück. Deine Durchschnittsgeschwindigkeit ist nicht 75 km/h, sondern das harmonische Mittel, was ca. 66,7 km/h ergibt.
- Formel:
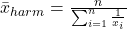

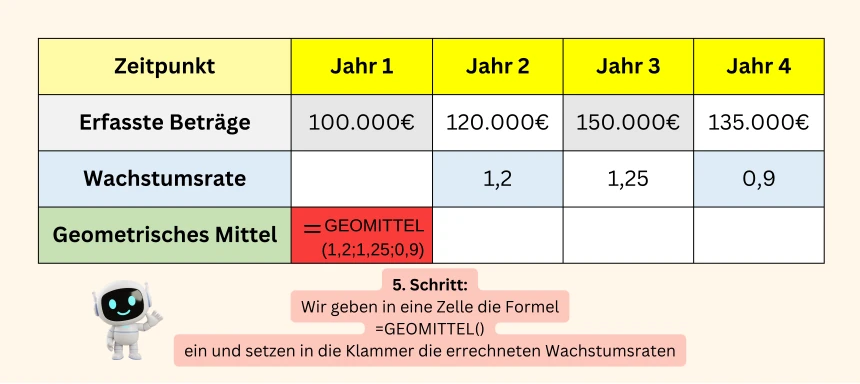
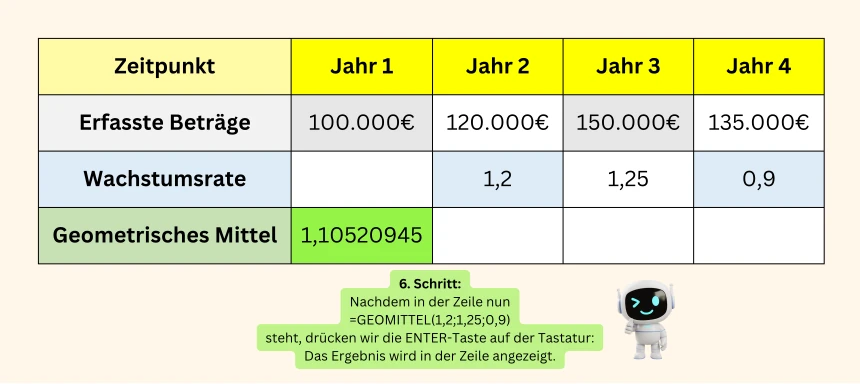
Das Geometrische Mittel mit Excel berechnen
Übungsaufgaben geometrisches Mittel
Hier findest du 3 Übungsaufgaben um dein Wissen zu festigen. Die Lösungen findest du darunter.
-
In der folgenden Tabelle findest du die Preise für Autoreifen. Berechne die mithilfe des geometrischen mittel die durchschnittliche prozentuale Veränderung.
|
Mai |
Juni |
Juli |
August |
September |
|
1,70 € |
1,90 € |
2,10 € |
2,30 € |
2,00 € |
Lösung
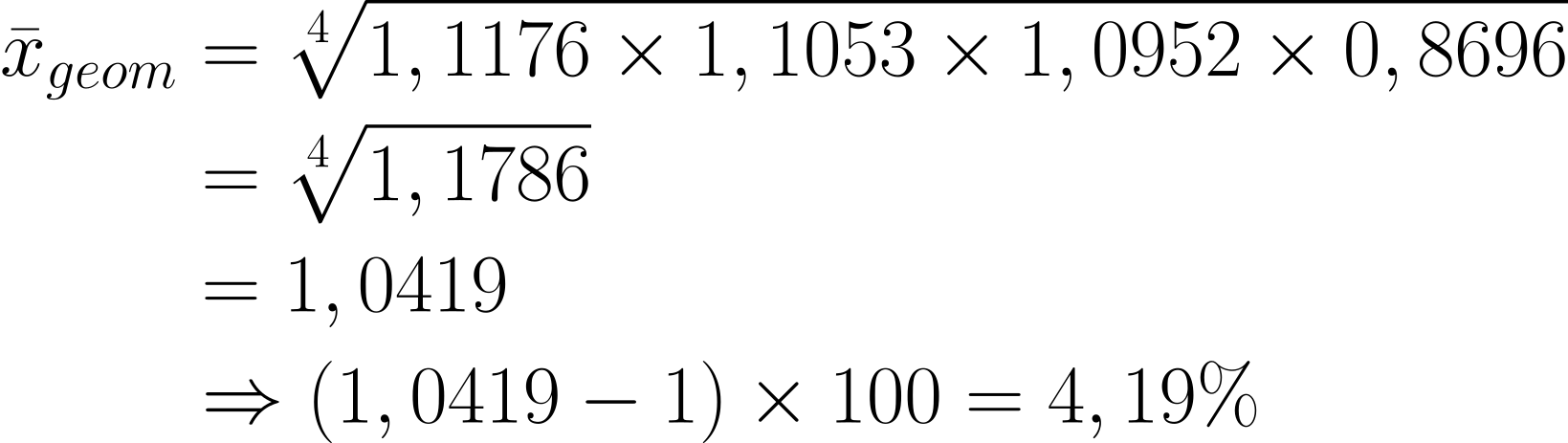
-
Durch die neuesten Subventionen von der “Grünen Partei”, sinken die Preise für Strom. Berechne die durchschnittliche prozentuale Veränderung.
|
September |
Oktober |
November |
Dezember |
Januar |
|
56,00 € |
53,57 € |
51,42 € |
49,87 € |
47, 84 € |
Lösung
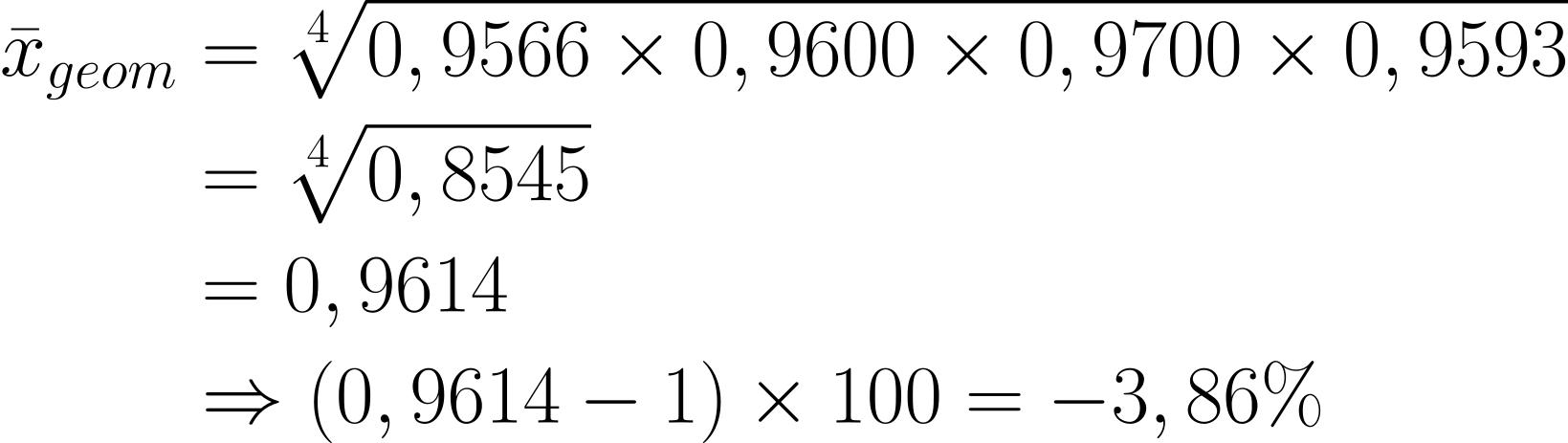
c) Der Big-Mac im Menü wird teurer. Berechne die durchschnittliche prozentuale Veränderung.
|
Mai |
Juni |
Juli |
August |
September |
|
12,99 € |
13,89 € |
12,99 € |
14,46 € |
12,99 € |
Lösung