(Noch keine Bewertungen)
Loading...
Vielleicht kennst du das Problem: Du sitzt vor einer Funktion und sollst die Definitionsmenge bestimmen – aber irgendwie wirkt alles verwirrend.
Was darf man einsetzen? Wo entstehen Fehler? Und warum ist die Definitionsmenge überhaupt so wichtig?
In diesem Ratgeber bekommst du eine leicht verständliche, Schritt-für-Schritt-Erklärung, wie du die Definitionsmenge sicher bestimmst und Beispiele richtig interpretierst
Lass uns direkt starten!
Die Definitionsmenge (auch: Definition domain) ist die Menge aller Zahlen, die man problemlos in eine Funktion einsetzen darf, ohne dass mathematische Fehler entstehen.
Das bedeutet: Alle Werte, für die die Funktion definiert ist, gehören zur Definitionsmenge. Wenn ein Wert zu einem Fehler wie einer Division durch Null oder einer negativen Zahl unter einer geraden Wurzel führt, gehört er nicht dazu.
Beispiel:
Bei der Funktion
darfst du nicht x = 3 einsetzen, da sonst eine Division durch Null entsteht.
Die Definitionsmenge ist also:
D = ℝ \ {3}
Definitionsmenge einer Funktion – Schritt für Schritt erklärt
Wenn du eine Definitionsmenge bestimmen willst, gehst du am besten systematisch vor. So übersiehst du keine kritischen Stellen und findest die Menge aller erlaubten x-Werte zuverlässig.
Zusammenhang zwischen Definitionsmenge und Funktion
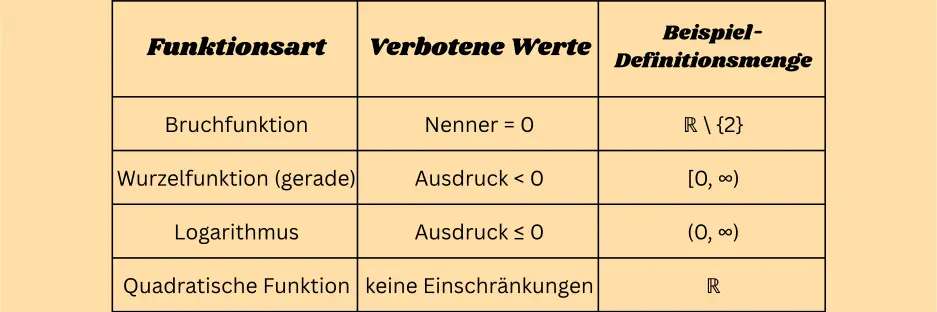
Die Art der Funktion bestimmt, welche Werte ausgeschlossen werden müssen.
Typische Problemstellen sind:
- Nenner = 0 → nicht erlaubt
- Wurzeln aus negativen Zahlen (bei geraden Wurzeln) → nicht erlaubt
- Logarithmen mit negativen Argumenten → nicht erlaubt
- Fakultäten von negativen Zahlen → nicht erlaubt
- Textaufgaben (realer Kontext) → oft gibt es zusätzliche Einschränkungen
Schritt-für-Schritt-Methode
Um die Definitionsmenge zuverlässig zu bestimmen, kannst du diese vier Schritte nutzen:
Schritt 1 – Problemstellen erkennen
Markiere alle kritischen Teile der Funktion: Brüche, Wurzeln, Logarithmen, Fakultäten oder andere spezielle Ausdrücke.
Schritt 2 – Bedingungen aufschreiben
Formuliere für jede Problemstelle die passende Bedingung:
- Bruch → Nenner ≠ 0
- Gerade Wurzel → Ausdruck ≥ 0
- Logarithmus → Argument > 0
Schritt 3 – Bedingungen lösen
Löse jede Gleichung oder Ungleichung einzeln.
Schritt 4 – Ergebnisse kombinieren und angeben
Kombiniere alle Einschränkungen (Schnittmengen, Ausschlüsse) und gib die Definitionsmenge in Intervall- oder Mengenschreibweise an.
Beispiel:
![\[f(x) = \frac { \sqrt{2x -4}} {x - 3}\]](https://www.nachhilfe-team.net/lernen-leicht-gemacht/wp-content/ql-cache/quicklatex.com-b987eef33c1708ba49923b894b35c56b_l3.png "Rendered by QuickLaTeX.com")
- Wurzel: 2x − 4 ≥ 0 → x ≥ 2
- Nenner: x − 3 ≠ 0 → x ≠ 3
Kombiniert: D = [2, ∞) \ {3}
Merksatz:
Die Definitionsmenge zeigt alle x-Werte, die erlaubt sind. Alles andere führt zu mathematischen Fehlern oder ist im realen Kontext nicht sinnvoll.
Definitionsmenge bestimmen – Methoden und Tipps
Damit du jede Definitionsmenge sicher findest, helfen dir diese Methoden:
1. Methode: Nenner untersuchen
Setze den Nenner gleich Null und schließe diese Werte aus.
Beispiel:
f(x) = 5 / (x² – 9)
x² – 9 = 0 → x = ±3
D = ℝ \ {–3, 3}
2. Methode: Wurzeln prüfen
Bei geraden Wurzeln gilt immer:
Ausdruck ≥ 0
3. Methode: Logarithmen beachten
Beim Logarithmus muss gelten:
Ausdruck > 0
4. Methode: Textkontexte beachten
Wenn z. B. eine Funktion Längen oder Zeit beschreibt, sind nur positive Werte sinnvoll.
Definitionsmenge angeben – so geht’s korrekt
In Mathematik wird die Definitionsmenge meist in Intervallschreibweise oder Mengendarstellung formuliert.
Beispiele für korrekte Schreibweisen:
- D = ℝ \ {2}
- D = [0, ∞)
- D = {x ∈ ℝ | x ≠ 5}
Definitionsmenge ausrechnen
Das „Ausrechnen“ der Definitionsmenge bedeutet, Einschränkungen mathematisch zu lösen.
Beispiel (mit Rechnung):
4 – x² ≥ 0
4 ≥ x²
|x| ≤ 2
D = [–2, 2]
Maximale Definitionsmenge – was ist das?
Die maximale Definitionsmenge umfasst alle Werte, die theoretisch für die Funktion erlaubt sind — ohne zusätzliche Einschränkungen aus Textaufgaben.
Beispiel:
Für 
ist die maximale Definitionsmenge:
Dₘₐₓ = [0, ∞)
Wenn in einer Aufgabe steht, dass x eine Entfernung beschreibt, bleibt die maximale Definitionsmenge gleich — aber die realistische Definitionsmenge könnte kleiner werden (z. B. nur x ≤ 100).
Die maximale Definitionsmenge hilft dir, den mathematischen Rahmen einer Funktion zu erkennen.
Definitionsmenge und Wertemenge – Unterschiede und Zusammenhänge
- Definitionsmenge: mögliche Eingaben (x-Werte)
- Wertemenge: mögliche Ausgaben (y-Werte oder Funktionswerte)
Die Definitionsmenge bestimmt also, welche Wertemenge überhaupt entstehen kann.
Beispiel:
Definition: x ≥ 0
Wertemenge: f(x) ≥ 0 → y ∈ [0, ∞)
Merksatz:
Die Definitionsmenge beeinflusst die Wertemenge – nie umgekehrt.
Definitionsmenge Schreibweise – mathematisch korrekt angeben
Wenn du eine Definitionsmenge angibst, benutzt du meistens Mengen- oder Intervallschreibweise. Wichtig ist zu verstehen, wofür die Symbole stehen:
ℝ
Bezeichnet die Menge aller reellen Zahlen. Dazu gehören ganze Zahlen, Brüche, endliche und unendliche Dezimalzahlen – also praktisch alles, was du auf einer Zahlengeraden finden kannst.
1. Intervalle
Intervalle geben an, welche Bereiche von ℝ erlaubt sind:
- [a, b] → geschlossenes Intervall: a und b inklusive
- (a, b) → offenes Intervall: a und b ausgeschlossen
- [a, b) oder (a, b] → Halb-offen
Beispiel:
[2, ∞) bedeutet: alle reellen Zahlen ab 2, einschließlich 2.
2. Mengenschreibweise
D = {x ∈ ℝ | x ≠ 2}
D = {x ∈ ℝ | x ≥ 0}
3. Ausschlüsse
Wenn bestimmte Werte nicht erlaubt sind, verwendest du:
ℝ \ {3} → alle reellen Zahlen außer 3.
Kombinationen
Manchmal musst du Intervalle und Ausschlüsse kombinieren, z. B.:
[2, ∞) \ {3} → alle Werte ab 2, aber 3 ist ausgeschlossen.
Fazit
Die Definitionsmenge ist ein grundlegendes Werkzeug, um Funktionen richtig zu verstehen und sicher damit zu arbeiten. Wenn du weißt, worauf du achten musst – Nenner, Wurzeln, Logarithmen und Kontext – kannst du jede Definitionsmenge schnell und korrekt bestimmen. Mit den Methoden und Beispielen aus diesem Artikel bist du bestens vorbereitet.
