Binomische Formeln gehören zu den Regeln in Mathe, die dir unglaublich viel Arbeit abnehmen können – vorausgesetzt, du weißt, wie sie funktionieren.
Genau das schauen wir uns in diesem Artikel gemeinsam an.
Du lernst, wie die drei binomischen Formeln aufgebaut sind, wie du sie sicher anhand von Beispielen anwendest und warum sie dir beim Rechnen mit Klammern so viel Zeit sparen.
Dieser Artikel bezieht sich nur auf die 3 binomischen Formeln, wenn du über binomische Formel hoch 3 lesen möchtest, klicke gerne auf die Links!
Die binomischen Formeln gehören zu den wichtigsten Grundlagen der Algebra und begegnen dir schon früh im Mathematikunterricht. Sie helfen dir dabei, Ausdrücke wie ![]() oder
oder ![]() schnell und ohne langes Ausmultiplizieren zu berechnen.
schnell und ohne langes Ausmultiplizieren zu berechnen.
Statt jeden Term einzeln auszurechnen, kannst du eine feste Regel anwenden, die immer funktioniert. Das spart Zeit, vermeidet Fehler und macht viele Aufgaben wesentlich übersichtlicher.
Wozu braucht man binomische Formeln – einfach erklärt
Du verwendest binomische Formeln in der Schule beim Ausmultiplizieren, beim Vereinfachen von Ausdrücken und beim Lösen von Gleichungen.
Später brauchst du sie auch in der Physik, Informatik oder in höheren Mathethemen, z. B. beim Umgang mit Funktionen oder beim Berechnen von Flächen.
Kurz gesagt: Binomische Formeln machen Rechnungen überschaubarer und zeigen dir wichtige Zusammenhänge zwischen Klammern und Quadraten.
Binomische Formel 1 – Erklärung der ersten binomischen Formel
Die erste binomische Formel lautet:
Sie zeigt dir, wie du eine Summe quadrierst. Statt das Produkt (a + b) mühsam auszumultiplizieren, kannst du direkt die drei Bestandteile nutzen:
- das Quadrat des ersten Terms
- zweimal das Produkt der beiden Terme
- das Quadrat des zweiten Terms
Durch die Formel erkennst du sofort die Struktur – das spart dir mehrere Zwischenschritte.
Binomische Formel 2 – Erklärung der zweiten binomischen Formel
Die zweite binomische Formel funktioniert ähnlich, nur dass du hier eine Differenz quadrierst:
Der einzige Unterschied: Das mittlere Glied wird negativ, weil ein Minus im Binom steht. Ansonsten bleibt das Muster gleich.
Diese Formel brauchst du besonders häufig beim Vereinfachen von Termen und beim Lösen quadratischer Gleichungen.
Binomische Formel 3 – Erklärung der dritten binomischen Formel
Die dritte binomische Formel beschreibt das Produkt einer Summe und einer Differenz:
Hier passiert Folgendes:
Beim Ausmultiplizieren heben sich die mittleren Terme gegenseitig auf. Deshalb bleiben am Ende nur die Quadrate von a und b übrig – mit einem Minus dazwischen.
Damit nutzt du die dritte binomische Formel:
Differenz mal Summe ergibt die Differenz der Quadrate.
Binomische Formel rechnen – Schritt-für-Schritt-Anleitung
Damit du sicher mit den binomischen Formeln umgehen kannst, findest du hier eine einfache Anleitung. Diese Schritte funktionieren immer – egal ob bei Zahlen oder Variablen.
1. Schritt: Erkenne die Struktur
Steht ein Quadrat dahinter? Sieht der Ausdruck wie (a + b) oder (a – b) aus? Entscheide, ob du Formel 1 oder 2 brauchst.
2. Schritt: Identifiziere die Terme
Überlege, was dein „a“ und was dein „b“ ist.
Beispiel: ![]()
→a=x, b=7
3. Schritt: Setze die Terme in die Formel ein
Nutze das Muster der passenden binomischen Formel.
4. Schritt: Rechne aus und vereinfache
Fasse zusammen, ordne Terme und vereinfache so weit wie möglich.
Binomische Formel faktorisieren
Manchmal willst du nicht ausmultiplizieren, sondern einen Ausdruck zurück in eine binomische Formel verwandeln. Das nennt man Faktorisieren.
Dabei gehst du so vor:
- Schau nach, ob der Term dem Muster der ersten oder zweiten binomischen Formel entspricht.
- Erkenne das Quadrat des ersten und zweiten Terms.
- Überprüfe, ob das mittlere Glied +2ab oder −2ab ist.
- Schreibe den Term wieder als Binom.
Binomische Formel Beispiele – Übungsaufgaben
Jetzt kannst du selber mal testen, ob du das Thema verstanden hast. Probiere die Übungsaufgaben zu lösen,.
Aufgabe 1
![]()
Aufgabe 2
![]()
Aufgabe 3
![]()
Aufgabe 4
![]()
Aufgabe 5
![]()
Aufgabe 6
![]()
Lösung Aufgabe 1
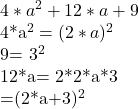
Lösung Aufgabe 2
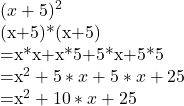
Lösung Aufgabe 3
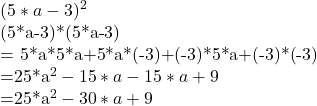
Lösung Aufgabe 4
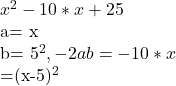
Lösung Aufgabe 5
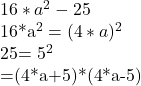
Lösung Aufgabe 6
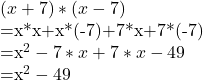
Fazit – das Wichtigste kurz zusammengefasst
Die binomischen Formeln gehören zu den wichtigsten Werkzeugen in der Algebra und helfen dir, Klammern schnell und fehlerfrei auszumultiplizieren oder Terme zu vereinfachen.
Besonders die erste und zweite binomische Formel begegnen dir täglich im Mathematikunterricht, bei Gleichungen, beim Ableiten und sogar in höheren mathematischen Zusammenhängen.
Wenn du erkennst, welches Muster dahintersteckt, sparst du Zeit und verstehst algebraische Strukturen viel besser.
Für weiterführende Fälle mit höheren Potenzen wie ![]() kannst du dich in dem verlinkten Artikel vertiefen.
kannst du dich in dem verlinkten Artikel vertiefen.